A Possible Model for the Price of Gold

One of the most controversial topics in investing is the price of gold. Eleven years ago, gold dropped as low as $252 per ounce. Since then, the yellow metal has risen more than five-fold, easily outpacing the major stock market indexes—and it seems to move higher every day.

Some goldbugs say this is only the beginning and that gold will soon break $2,000, then $5,000 and then $10,000 per ounce.

But the question is, “How can anyone reasonably calculate what the price of gold is?” For stocks, we have all sorts of ratios. Sure, those ratios can be off…but at least they’re something. With gold, we have nothing. After all, gold is just a rock (ok ok, an element).

How the heck can we even begin to analyze gold’s value? There’s an old joke that the price of gold is understood by exactly two people in the entire world. They both work for the Bank of England and they disagree.

In this post, I want to put forth a possible model for evaluating the price of gold. The purpose of the model isn’t to say where gold will go but to look at the underlying factors that drive gold. Let me caution that as with any model, this model has its flaws, but that doesn’t mean it isn’t useful.

The key to understanding the gold market is to understand that it’s not really about gold at all. Instead, it’s about currencies, and in our case that means the dollar. Gold is really the anti-currency. It serves a valuable purpose in that it keeps all the other currencies honest (or exposes their dishonesty).

This may sound odd but every currency has an interest rate tied to it. In essence, that interest rate is what the currency is all about. All those dollar bills in your wallet have an interest rate tied to them. The euro, the pound and the yen also all have interest rates tied to them.

Before I get to my model, I want to take a step back for a moment and discuss a strange paradox in economics known as Gibson’s Paradox. This is one the most puzzling topics in economics. Gibson’s Paradox is the observation that interest rates tend to follow the general price level and not the rate of inflation. That’s very strange because it seems obvious that as inflation rises, interest rates ought to keep up. And as inflation falls back, rates should move back as well. But historically, that wasn’t the case.

Instead, interest rates rose as prices rose, and rates only fell when there was deflation. This paradox has totally baffled economists for years. Yet it really does exist. John Maynard Keynes called it “one of the most completely established empirical facts in the whole field of quantitative economics.” Milton Friedman and Anna Schwartz said that “the Gibsonian Paradox remains an empirical phenomenon without a theoretical explanation.”

Even many of today’s prominent economists have tried to tackle Gibson’s Paradox. In 1977, Robert Shiller and Jeremy Siegel wrote a paper on the topic. In 1988 Robert Barsky and none other than Larry Summers took on the paradox in their paper “Gibson’s Paradox and the Gold Standard,” and it’s this paper that I want to focus on. (By the way, in this paper the authors thank future econobloggers Greg Mankiw and Brad DeLong.)

Summers and Barsky explain that the Gibson Paradox does indeed exist. They also say that it’s not connected with nominal interest rates but with real (meaning after-inflation) interest rates. The catch is that the paradox only works under a gold standard. Once the gold standard is gone, the Gibson Paradox fades away.

It’s my hypothesis that Summers and Barsky are on to something and that we can use their insight to build a model for the price of gold. The key is that gold is tied to real interest rates. Where I differ from them is that I use real short-term interest rates whereas they focused on long-term rates.

Here’s how it works. I’ve done some back-testing and found that the magic number is 2% (I’m dumbing this down for ease of explanation). Whenever the dollar’s real short-term interest rate is below 2%, gold rallies. Whenever the real short-term rate is above 2%, the price of gold falls. Gold holds steady at the equilibrium rate of 2%. It’s my contention that this was what the Gibson Paradox was all about since the price of gold was tied to the general price level.

Now here’s the kicker: there’s a lot of volatility in this relationship. According to my backtest, for every one percentage point real rates differ from 2%, gold moves by eight times that amount per year. So if the real rates are at 1%, gold will move up at an 8% annualized rate. If real rates are at 0%, then gold will move up at a 16% rate (that’s been about the story for the past decade). Conversely, if the real rate jumps to 3%, then gold will drop at an 8% rate.

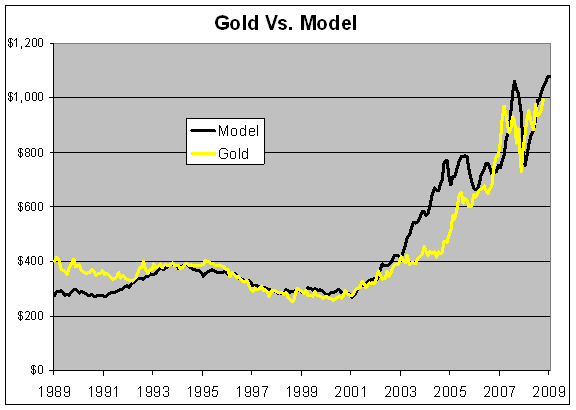
Here’s what the model looks like against gold over the past two decades:

The relationship isn’t perfect but it’s held up fairly well over the past 15 years or so. The same dynamic seems at work in the 15 years before that, but I think the ratios are different.

In effect, gold acts like a highly-leveraged short position in U.S. Treasury bills and the breakeven point is 2% (or more precisely, a short on short-term TIPs).

Let me make this clear that this is just a model and I’m not trying to explain 100% of gold’s movement. Gold is subject to a high degree of volatility and speculation. Geopolitical events, for example, can impact the price of gold. I would also imagine that at some point, gold could break a replacement price where it became so expensive that another commodity would replace its function in industry, and the price would suffer.

Instead of explaining all of gold, my aim is to pinpoint the underlying factors that are strongly correlated with gold. The number and ratios I used (2% break-even and 8-to-1 ratio) seem to have the strongest correlation for recent history. How did I arrive at them? Simple trial and error. The true numbers may be off and I’ll leave the fine-tuning for someone else.

In my view, there are a few key takeaways.

The first and perhaps the most significant is that gold isn’t tied to inflation. It’s tied to low real rates which are often the by-product of inflation. Right now we have rising gold and low inflation. This isn’t a contradiction. (John Hempton wrote about this recently.)

The second point is that when real rates are low, the price of gold can rise very, very rapidly.

The third is that when real rates are high, gold can fall very, very quickly.

Fourth, there’s no reason for there to be a relationship between equity prices and gold (like the Dow-to-gold ratio).

Fifth, the TIPs yield curve indicates that low real rates may last for a few more years.

The final point is that the price of gold is essentially political. If a central banker has the will to raise real rates as Volcker did 30 years ago, then the price of gold can be crushed.

Technical note: If you want to see how the heck I got these numbers, please see this spreadsheet.

Column A is the date.
Column B is an index of real returns for T-bills I got from the latest Ibbotson Yearbook. It goes through the end of last year.
Column C is a 2% trendline.
Column D is adjusting B by C.
Column E is inverting Column D since we’re shorting.
Column F computes the monthly change the levered up 8-to-1.
Column G is the Model with a starting price of $275 (in red).
Column H is the price of gold. It goes up to last September.

Posted by on October 6th, 2010 at 8:15 am


The information in this blog post represents my own opinions and does not contain a recommendation for any particular security or investment. I or my affiliates may hold positions or other interests in securities mentioned in the Blog, please see my Disclaimer page for my full disclaimer.