Gold Hits All-Time High
The price of gold recently broke out to a new all-time high of $1,440.32. To commemorate this milestone I’m re-running of my most linked-to posts ever on a possible model for how to price gold. Jake at EconomPicData was kind enough to make a longer-term chart of our model.
One of the most controversial topics in investing is the price of gold. Eleven years ago, gold dropped as low as $252 per ounce. Since then, the yellow metal has risen more than five-fold, easily outpacing the major stock market indexes—and it seems to move higher every day.
Some goldbugs say this is only the beginning and that gold will soon break $2,000, then $5,000 and then $10,000 per ounce.
But the important question is, “How can anyone reasonably calculate what the price of gold is?” For stocks, we have all sorts of ratios. Sure, those ratios can be off…but at least they’re something. With gold, we have nothing. After all, gold is just a rock (ok ok, an element).
How the heck can we even begin to analyze gold’s value? There’s an old joke that the price of gold is understood by exactly two people in the entire world. They both work for the Bank of England and they disagree.
In this post, I want to put forth a possible model for evaluating the price of gold. The purpose of the model isn’t to say where gold will go but to look at the underlying factors that drive gold. Let me caution that as with any model, this model has its flaws, but that doesn’t mean it isn’t useful.
The key to understanding the gold market is to understand that it’s not really about gold at all. Instead, it’s about currencies, and in our case that means the dollar. Gold is really the anti-currency. It serves a valuable purpose in that it keeps all the other currencies honest (or exposes their dishonesty).
This may sound odd, but every currency has an interest rate tied to it. In essence, that interest rate is what the currency is all about. All those dollar bills in your wallet have an interest rate tied to them. The euro, the pound and the yen also all have interest rates tied to them.
Before I get to my model, I want to take a step back for a moment and discuss a strange paradox in economics known as Gibson’s Paradox. This is one the most puzzling topics in economics. Gibson’s Paradox is the observation that interest rates tend to follow the general price level and not the rate of inflation. That’s very strange because it seems obvious that as inflation rises, interest rates ought to keep up. And as inflation falls back, rates should move back as well. But historically, that wasn’t the case.
Instead, interest rates rose as prices rose, and rates only fell when there was deflation. This paradox has totally baffled economists for years. Yet it really does exist. John Maynard Keynes called it “one of the most completely established empirical facts in the whole field of quantitative economics.” Milton Friedman and Anna Schwartz said that “the Gibsonian Paradox remains an empirical phenomenon without a theoretical explanation.”
Even many of today’s prominent economists have tried to tackle Gibson’s Paradox. In 1977, Robert Shiller and Jeremy Siegel wrote a paper on the topic. In 1988 Robert Barsky and none other than Larry Summers took on the paradox in their paper “Gibson’s Paradox and the Gold Standard,” and it’s this paper that I want to focus on. (By the way, in this paper the authors thank future econobloggers Greg Mankiw and Brad DeLong.)
Summers and Barsky explain that the Gibson Paradox does indeed exist. They also say that it’s not connected with nominal interest rates but with real (meaning after-inflation) interest rates. The catch is that the paradox only works under a gold standard. Once the gold standard is gone, the Gibson Paradox fades away.
It’s my hypothesis that Summers and Barsky are on to something and that we can use their insight to build a model for the price of gold. The key is that gold is tied to real interest rates. I differ from them in that I use real short-term interest rates whereas they focused on long-term rates.
Here’s how it works. I’ve done some back-testing and found that the magic number is 2% (I’m dumbing this down for ease of explanation). Whenever the dollar’s real short-term interest rate is below 2%, gold rallies. Whenever the real short-term rate is above 2%, the price of gold falls. Gold holds steady at the equilibrium rate of 2%. It’s my contention that this was what the Gibson Paradox was all about since the price of gold was tied to the general price level.
Now here’s the kicker: there’s a lot of volatility in this relationship. According to my backtest, for every one percentage point real rates differ from 2%, gold moves by eight times that amount per year. So if the real rates are at 1%, gold will move up at an 8% annualized rate. If real rates are at 0%, then gold will move up at a 16% rate (that’s been about the story for the past decade). Conversely, if the real rate jumps to 3%, gold will drop at an 8% rate.
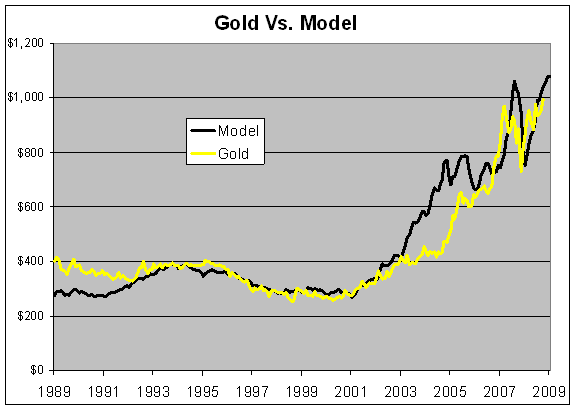
Here’s what the model looks like against gold over the past two decades:
The relationship isn’t perfect but it’s held up fairly well over the past 15 years or so. The same dynamic seems at work in the 15 years before that, but I think the ratios are different.
In effect, gold acts like a highly-leveraged short position in U.S. Treasury bills and the breakeven point is 2% (or more precisely, a short on short-term TIPs).
Let me make clear that this is just a model and that I’m not trying to explain 100% of gold’s movement. Gold is subject to a high degree of volatility and speculation. Geopolitical events, for example, can impact the price of gold. I would also imagine that at some point, gold could break a replacement price where it became so expensive that another commodity would replace its function in industry, and the price would suffer.
Instead of trying to explain all of gold, my aim is to pinpoint the underlying factors that are strongly correlated with gold. The number and ratio I used (2% break-even and 8-to-1 ratio) seem to have the strongest correlation for recent history. How did I arrive at them? Simple trial and error. The true numbers may be off and I’ll leave the fine-tuning to someone else.
In my view, there are a few key takeaways.
The first and perhaps the most significant is that gold isn’t tied to inflation. It’s tied to low real rates which are often the by-product of inflation. Right now we have rising gold and low inflation. This isn’t a contradiction. (John Hempton wrote about this recently.)
The second point is that when real rates are low, the price of gold can rise very, very rapidly.
The third point is that when real rates are high, gold can fall very, very quickly.
Fourth, there’s no reason for there to be a relationship between equity prices and gold (like the Dow-to-gold ratio).
Fifth, the TIPs yield curve indicates that low real rates may last for a few more years.
The final point is that the price of gold is essentially political. If a central banker has the will to raise real rates as Volcker did 30 years ago, the price of gold can be crushed.
Technical note: If you want to see how the heck I got these numbers, please see this spreadsheet.
Column A is the date.
Column B is an index of real returns for T-bills I got from the latest Ibbotson Yearbook. It goes through the end of last year.
Column C is a 2% trendline.
Column D is adjusting B by C.
Column E is inverting Column D since we’re shorting.
Column F computes the monthly change levered up 8-to-1.
Column G is the Model with a starting price of $275 (in red).
Column H is the price of gold. It goes up to last September.
Posted by Eddy Elfenbein on March 3rd, 2011 at 9:27 am
The information in this blog post represents my own opinions and does not contain a recommendation for any particular security or investment. I or my affiliates may hold positions or other interests in securities mentioned in the Blog, please see my Disclaimer page for my full disclaimer.
-
-
Archives
- April 2025
- March 2025
- February 2025
- January 2025
- December 2024
- November 2024
- October 2024
- September 2024
- August 2024
- July 2024
- June 2024
- May 2024
- April 2024
- March 2024
- February 2024
- January 2024
- December 2023
- November 2023
- October 2023
- September 2023
- August 2023
- July 2023
- June 2023
- May 2023
- April 2023
- March 2023
- February 2023
- January 2023
- December 2022
- November 2022
- October 2022
- September 2022
- August 2022
- July 2022
- June 2022
- May 2022
- April 2022
- March 2022
- February 2022
- January 2022
- December 2021
- November 2021
- October 2021
- September 2021
- August 2021
- July 2021
- June 2021
- May 2021
- April 2021
- March 2021
- February 2021
- January 2021
- December 2020
- November 2020
- October 2020
- September 2020
- August 2020
- July 2020
- June 2020
- May 2020
- April 2020
- March 2020
- February 2020
- January 2020
- December 2019
- November 2019
- October 2019
- September 2019
- August 2019
- July 2019
- June 2019
- May 2019
- April 2019
- March 2019
- February 2019
- January 2019
- December 2018
- November 2018
- October 2018
- September 2018
- August 2018
- July 2018
- June 2018
- May 2018
- April 2018
- March 2018
- February 2018
- January 2018
- December 2017
- November 2017
- October 2017
- September 2017
- August 2017
- July 2017
- June 2017
- May 2017
- April 2017
- March 2017
- February 2017
- January 2017
- December 2016
- November 2016
- October 2016
- September 2016
- August 2016
- July 2016
- June 2016
- May 2016
- April 2016
- March 2016
- February 2016
- January 2016
- December 2015
- November 2015
- October 2015
- September 2015
- August 2015
- July 2015
- June 2015
- May 2015
- April 2015
- March 2015
- February 2015
- January 2015
- December 2014
- November 2014
- October 2014
- September 2014
- August 2014
- July 2014
- June 2014
- May 2014
- April 2014
- March 2014
- February 2014
- January 2014
- December 2013
- November 2013
- October 2013
- September 2013
- August 2013
- July 2013
- June 2013
- May 2013
- April 2013
- March 2013
- February 2013
- January 2013
- December 2012
- November 2012
- October 2012
- September 2012
- August 2012
- July 2012
- June 2012
- May 2012
- April 2012
- March 2012
- February 2012
- January 2012
- December 2011
- November 2011
- October 2011
- September 2011
- August 2011
- July 2011
- June 2011
- May 2011
- April 2011
- March 2011
- February 2011
- January 2011
- December 2010
- November 2010
- October 2010
- September 2010
- August 2010
- July 2010
- June 2010
- May 2010
- April 2010
- March 2010
- February 2010
- January 2010
- December 2009
- November 2009
- October 2009
- September 2009
- August 2009
- July 2009
- June 2009
- May 2009
- April 2009
- March 2009
- February 2009
- January 2009
- December 2008
- November 2008
- October 2008
- September 2008
- August 2008
- July 2008
- June 2008
- May 2008
- April 2008
- March 2008
- February 2008
- January 2008
- December 2007
- November 2007
- October 2007
- September 2007
- August 2007
- July 2007
- June 2007
- May 2007
- April 2007
- March 2007
- February 2007
- January 2007
- December 2006
- November 2006
- October 2006
- September 2006
- August 2006
- July 2006
- June 2006
- May 2006
- April 2006
- March 2006
- February 2006
- January 2006
- December 2005
- November 2005
- October 2005
- September 2005
- August 2005
- July 2005
 Eddy Elfenbein is a Washington, DC-based speaker, portfolio manager and editor of the blog Crossing Wall Street. His
Eddy Elfenbein is a Washington, DC-based speaker, portfolio manager and editor of the blog Crossing Wall Street. His